Sukhdev Roy* and K. P. J. Reddy^†,**

*Department of Physics and Computer Science, Dayalbagh Educational Institute, Agra 282 005, India

†Department of Aerospace Engineering, Indian Institute of Science, Bangalore 560 012, India

A simplified model for the complex photocycle of the D85N genetic variant of the bacteriorhodopsin (bR) protein molecule is presented. Steady state population densities of the various intermediate states of the molecule induced by photo-absorption of modulation light beam are obtained using the rate equations approach. All-optical modulation of various probe signals at wavelengths corresponding to absorption peaks of each of the intermediate states by a pump signal at 570 nm is presented in the form of optical densities. The analysis presented here is useful for designing the molecular spatial light modulators using D85N variant of bR molecules.

---

RECENT years have witnessed dramatic progress in investigating novel materials for all-optical signal processing and data storage. The photochromic protein bacteriorhodopsin (bR) which is found in the purple membrane of Halobacterium halobium, has emerged as an excellent material for bio-molecular photonic applications due to its unique advantages¹. bR absorbs light in a bacterium and undergoes a complex photocycle that generates intermediate states with absorption maxima spanning the entire visible region of the spectrum. It has a high quantum efficiency of converting light into a state change and large absorption cross-section. The crystal-like architecture leads to high stability and makes it

**For correspondence. (e-mail: laser@aero.iisc.ernet.in)

robust to degeneration by environmental perturbations. Thin bR films in polymers and gels have been switched between two stable states more than a million times without any photodegradation.

The photocycle of the bR molecule can be readily modified by replacing the light absorbing component of the protein which is a retinal (Vitamin-A-like) chromophore, by natural and synthetic analogues, thereby shifting to virtually any colour. Also, genetic mutations of bR through biotechnological procedures such as variation in polymer environment including pH and degree of hydration, can alter both the kinetic and spectral properties of bR. Furthermore, the low cost of production, low power requirements and it being environmentally friendly have made bR an attractive photonic material^2,3. Many nonlinear optical phenomena including two-photon absorption³, second harmonic generation⁴, saturable absorption^5,6, wave mixing and phase conjugation⁶ and optical bistability⁷ have been reported in bR molecules. Based on these phenomena bR molecules have been used for many applications including mode-locking⁸, switching⁹, neural networks¹⁰, spatial light modulation^11–13, spatial frequency filtering¹⁴, logic gates¹⁵, dynamic holography¹⁶ and biochips for optical computers using 3D optical memories³.

The bR molecule contains seven transmembrane helical segments and consists of a polypeptide chain composed of 248 amino acids. The active chromophore in the bR protein is a retinal molecule linked via a protonated Schiff base near the middle of helix G to lysine 216. The relevant location for the proton pumping activity of the bR protein consists of an ion pair which is composed of a protonated Schiff base and an anionic aspartic acid in position 85 (Asp85 residue). Proton transfer from the Schiff base to Asp85 is the primary mechanism in the feeding protons towards the extracellular side of the membrane and other proton transfers. This mechanism is also associated with conformational changes in the bR molecule and its chromorphoric group during the photocycle^1,2. Variation of the polymer environment including pH and degree of hydration can lead to dramatic changes in optical performance¹⁷. For permanent optical storage applications, a mutant is needed in which an intermediate state occurs with a lifetime of several years. At pH 5–7 with glycerol as a less protic solvent, protonation of the Asp85 residue results in the photoexcitation of the all-trans configuration into a state with 9-cis configuration with red light, which is thermally stable and is no longer catalysed to transform to the all-trans configuration of the initial state. Thus, a photoexcitation leads to a short circuit in the photocycle. This 9-cis configuration photoproduct is called the P-state. It absorbs at 490 nm and can be photochemically reconverted to the initial state¹⁸. The P-state is thermally stable at room temperature leading to no thermal pathway to reconvert itself to the initial B-state and hence can be used for permanent optical storage^19,20.

The aim of this communication is to present a simplified model for the complex photocycle of the D85N variant of bR which has a thermally stable P- (and Q) state. Based on this model the photocycle is analysed using the rate equation approach and analytical expressions are derived for the transmission characteristics of the bR film for probe beams at various wavelengths. These characteristics are useful in designing the molecular spatial light modulators based on different intermediate states of the D85N variant of bR molecule. However, no attempt has been made to study the SLM properties of this variant in the present communication.

The photocyle^12,18,21 of the bR molecule is shown schematically in Figure 1 a. In the initial B-state, also called the light adapted state, the retinal chromophore is in its all-trans molecular configuration. After excitation with yellow light at 570 nm, the molecule in the initial bR state gets transformed into the J-state with an absorption maximum at ~ 650 nm within about 450 fs. The species in the J-state thermally transform in 3 ps into the intermediate K-state which in turn transforms in 2 m s into the L-state. The relatively long-lived intermediate M-state is generated by thermal relaxation of species from the L-state in 50 m s. The molecule returns to the B-state via a couple of intermediate states N and O through thermal relaxation in about 10 ms. From the all-trans configuration of O, the P-state is formed in a photochemical transition induced with red light. In the dark, a thermal decomposition of the P-state into the Q product takes place. There is no thermal decay from the P- or Q-state to the initial B-state and the initial B-state can be generated only through photochemical excitation of the P- and Q-states¹⁸.

We introduce a simplified level diagram (Figure 1 b) to represent the photochemical cycle of bR molecules, which enables adoption of the simple rate equation approach for the population densities in the various intermediate states. An important feature of all the intermediates is their ability to be photochemically switched back to the initial B-state by shining light at a wavelength that corresponds to the absorption peak of the intermediate in question. The wavelength (in nm) of the absorption peak of each species is shown as a subscript in Figure 1.

In the simplified model the states B, L, K, M, N, O and P(Q) of bR are represented by numbers 1–7, respectively. The total bR population in the medium is

N =

where N_i is the population densities of intermediate states. We assume that a medium containing bR

a

 

b

 

Figure 1. a, Photocycle of D85N variant of bacteriorhodopsin; b, equivalent simplified model; Subscripts indicate absorption peaks in nm. The solid and dashed arrows indicate thermal decay and photoinduced transitions, respectively.

molecules is exposed to a light beam of intensity Ią _m, which modulates the population densities of different states through excitation and de-excitation processes. These light intensity-induced population changes are described by the rate equations in the operator form,

(1)

The rate equations for the different states can be written and the intensity-dependent absorption coefficient incorporating all the photochromic processes in the photocyle can be derived analytically which will be reported elsewhere. In this communication, we consider the modulation of different laser probe beam transmissions by the modulation beam intensity-induced population changes as experimentally reported by Popp et al.¹⁸. Propagation effects on the modulating light beam are ignored in the following analysis by assuming optically thin bR samples.

The modulation-induced population densities for the various states at steady state are given by,

(ką ₂ką _{3s 1y 13}I_m)^–1

(ką ₂)^–1

(ką ₂ką ₃)^–1

N_i = N₁(ką ₂ką _{3s 1y 13}I_m) ką ₄(k₄)^–1 , (2)

 

ką ₄ką ₅(k₅)^–1

ką ₄ką ₅ką ₆(k₆)^–1

ką ₄ką ₅ką _{6s 6y 67}(k_{6s 7})^–1

where N₁ = N/X, and

X = 1 + ką _{3s 1}(l _m)y ₁₃I_m(k₃)^–1{1 + k₃ką ₂(k₂)^–1

[1 + k₂ką ₄ (k₄)^–1 (1 + k₄ką ₅(k₅)^–1

[1 + k₅ką ₆(k₆)^–1(1 + s _{6y 67}(s ₇)^–1)])]}. (3)

 

Here, ką _i = k_i/(k_i + s _iI_m) for i = 2, 4, 5, ką ₃ = k₃/(k₃ +
s _{3y 31}I_m), ką ₆ = k₆/(k₆ + s _{6y 67}I_m) and s _i, i = 1–7 are the absorption cross-sections of the states B, L, K, M, N, O and P, respectively. I_m is the photon density flux of the modulation laser beam (ratio of the intensity Ią _m, to the photon energy hn ) and y ₁₃ = 0.64, y ₃₁ = 0.64 and y ₆₇ = 0.02 are the quantum efficiencies for the transitions B  K, K  B and O  P, respectively²¹. Detailed description of the symbols used in the analysis is presented in an earlier paper¹². Numerical values of the rate constants and absorption cross-sections for different levels are given in Table 1.

Spatial light modulators (SLMs) are the important key elements in real-time optical signal processing, computing and information processing systems. The feasibility of using bR molecules for the development of a molecular SLM depends on the ability to modulate the weak probe signal by the intensity-dependent population induced by the modulation laser beam. Hence we present the modulation characteristics for various intermediates of the bR molecule. We consider laser probe beams of intensity Ią _p (<< Ią _m) at different wavelengths corresponding to the absorption maximum of the states M, P, B and O, separately. The propagation of the probe beam through the bR medium is governed by

(4)

where x is the distance in the medium and a _p is the absorption coefficient at the probe wavelength. Based on the absorption spectra of the various intermediate

a

b

 

c

d

 

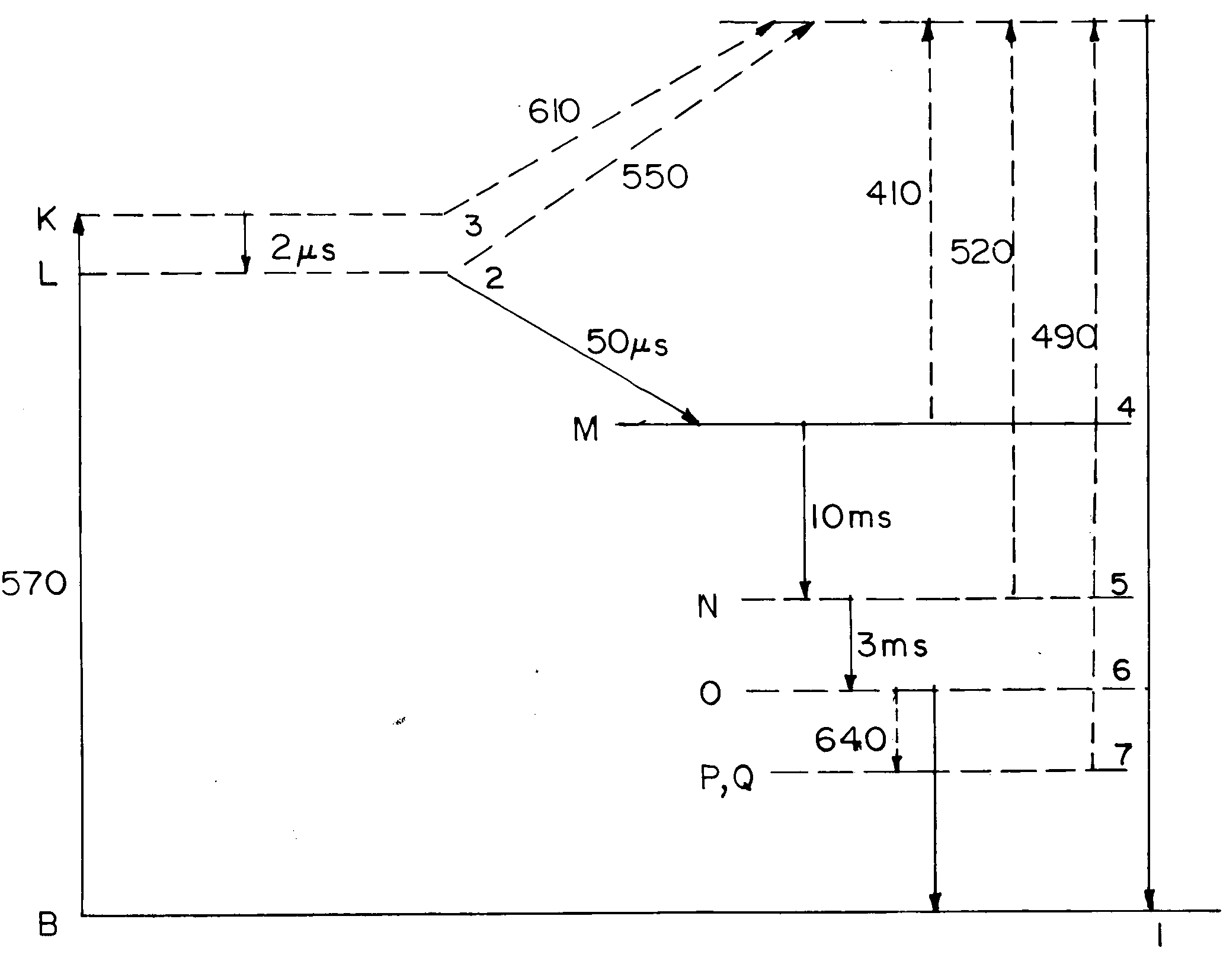
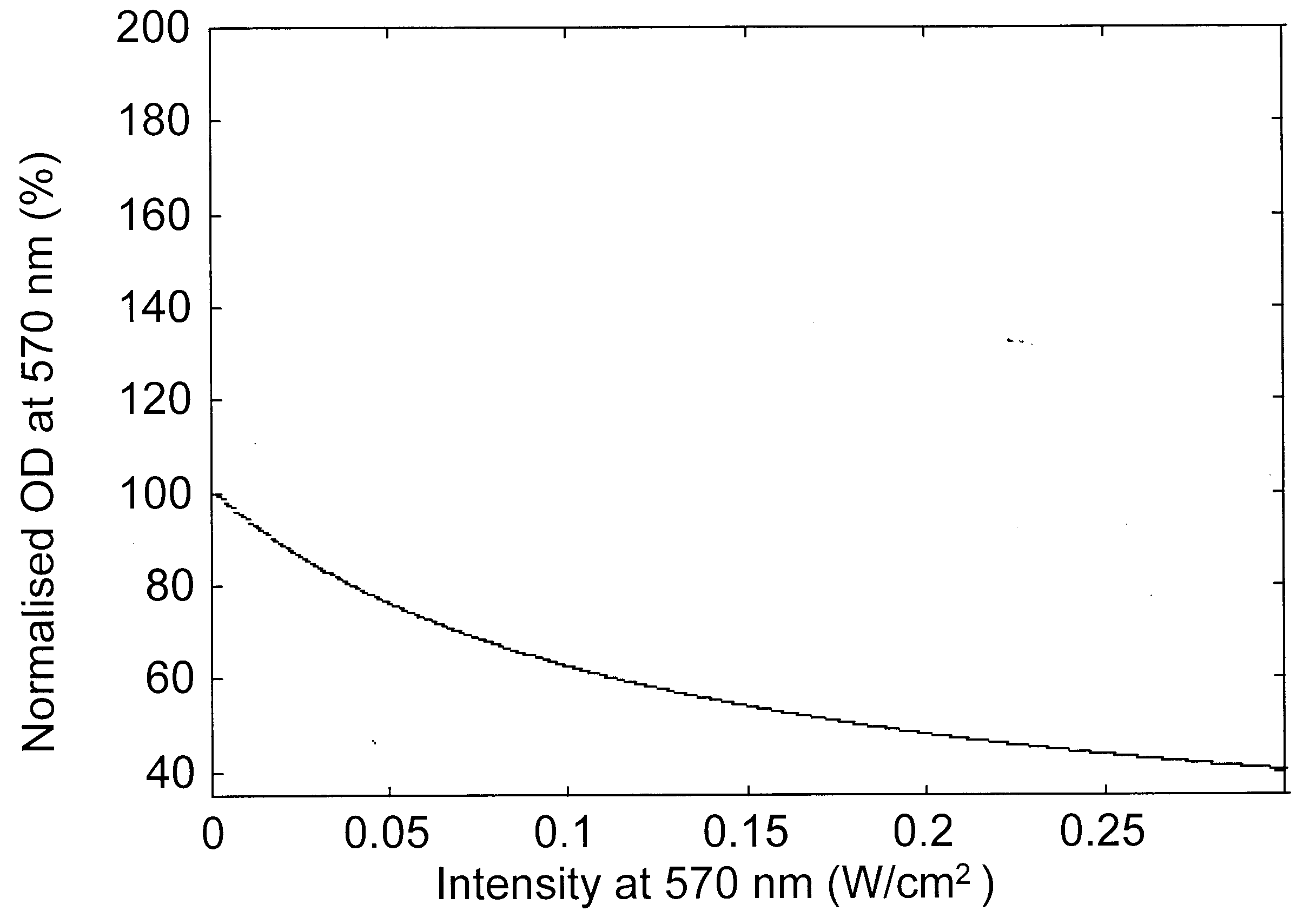
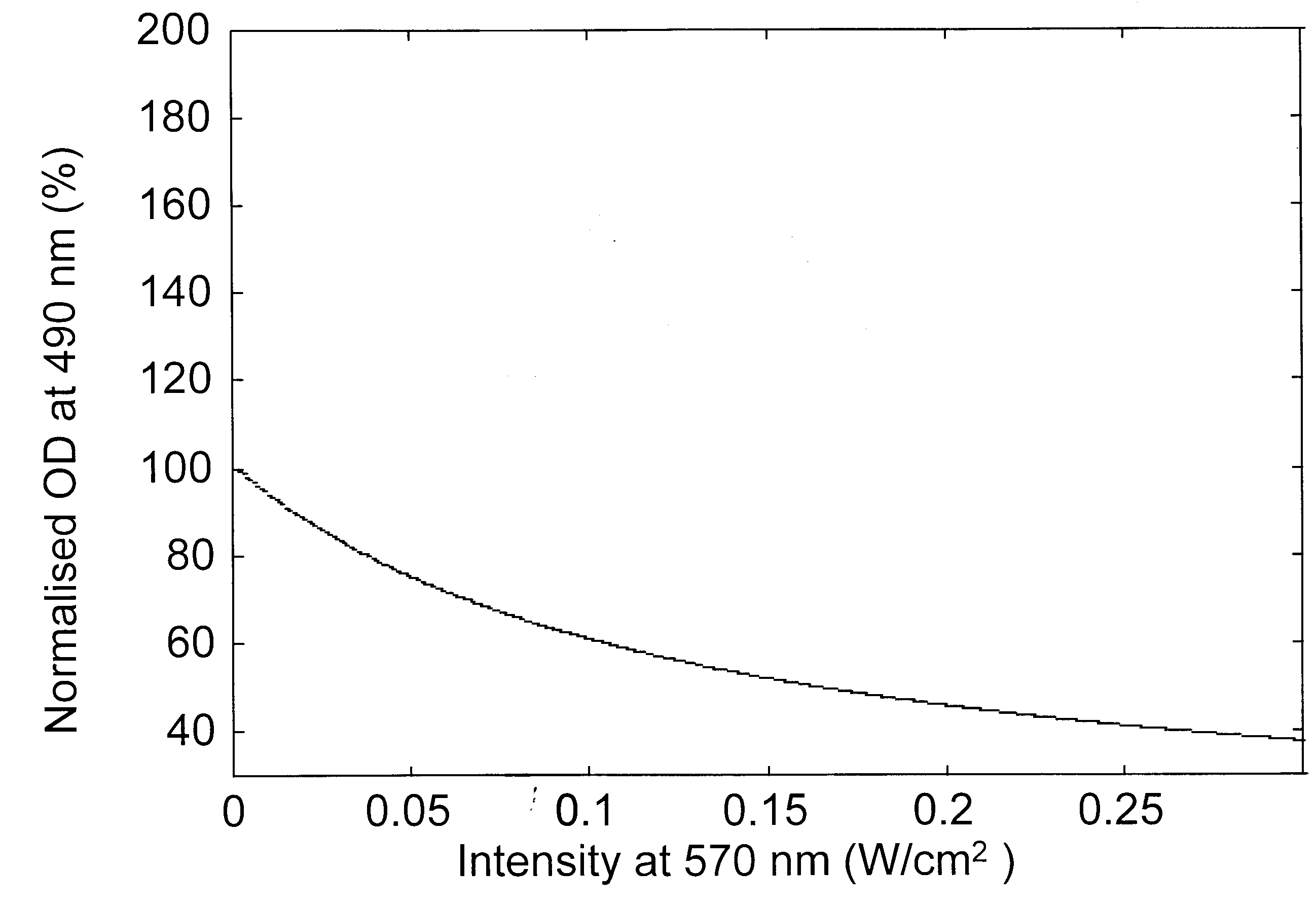
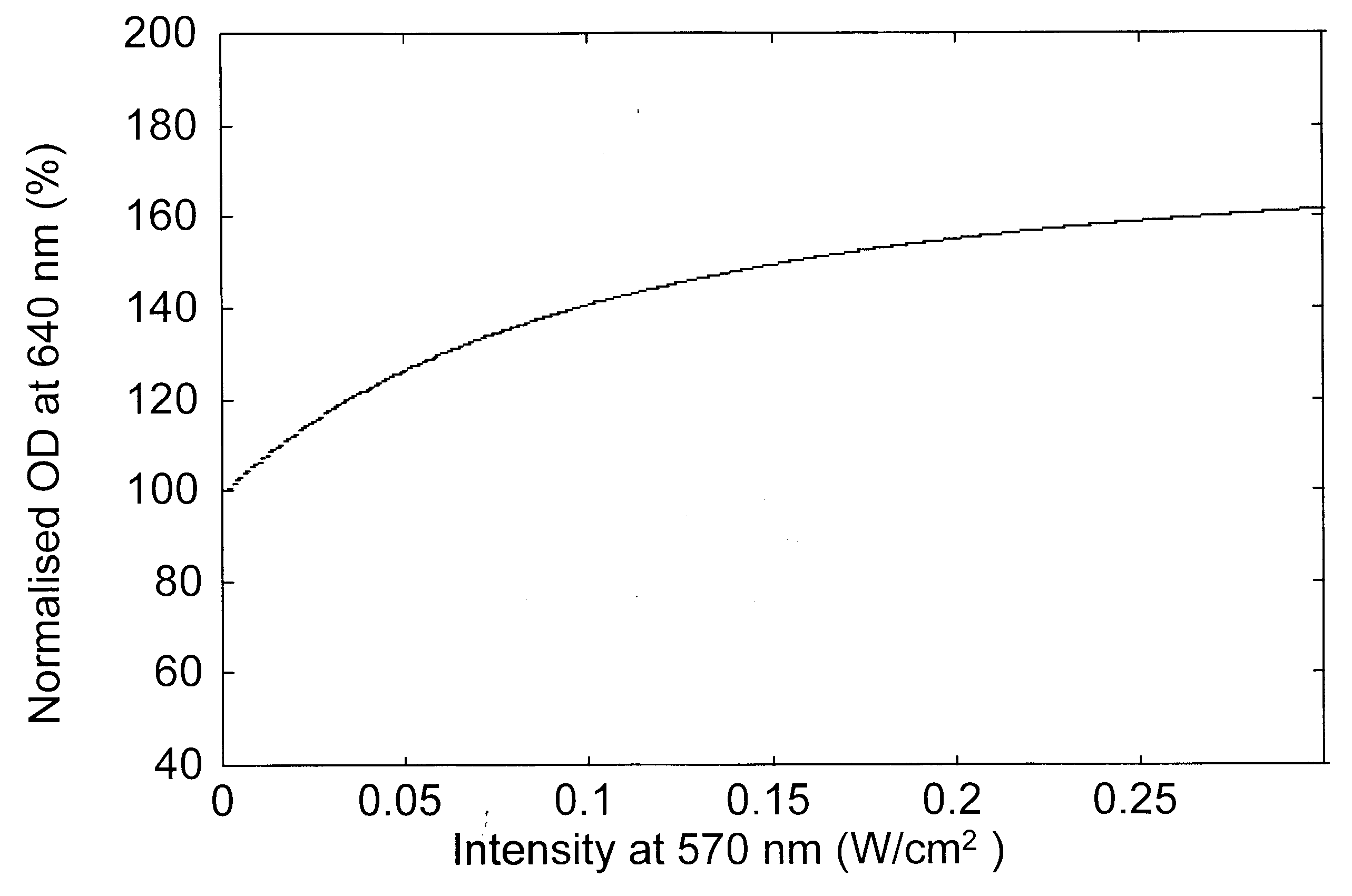
Figure 2. Variation of the modulation beam intensity-dependent normalized optical density for a probe beam at a, 570 nm; b, 490 nm; c, 410 nm and d, 640 nm.

states^18,20–23, the absorption coefficient for the respective probe beams can be written in terms of the population densities of the participating intermediate states, as shown in Table 2. The modulation characteristics for different probe beams can be computed by integrating eq. (4) using corresponding absorption coefficients. The results in the form of ratio of the transmitted to the incident probe beam intensity for various probe beams are given in Table 2. The modulation characteristics are also computed in terms of optical densities (OD) of the bR film defined as²⁴

OD = –log₁₀(I_pout/I_pin). (5)

Modulation laser beam intensity-dependent variation of the absorption changes of various probe beams is presented in Figure 2 a–d, for a bR film with an initial OD of 3.3 (ref. 18) at 570 nm. The absorption changes are given as per cent of the initial absorption at the respective probe wavelength and as a function of the intensity of the pump (modulation) beam. These figures indicate that as the modulation beam intensity at 570 nm is raised from 0.5 to 300 mW/cm², the absorption of the probe beams at 570 and 490 nm decreased while it increased at 410 and 640 nm. The decrease in absorption at 570 nm indicates that the population in the initial B-state decreased as the modulation beam intensity increased with corresponding increase in the photoconversion. In absence of the 640 nm wavelength, the population of the P-state is very low and the absorption of the probe beam is essentially dominated by the broad band absorption of the molecules in the B-state. Hence the decrease of absorption of the probe beam at 490 nm is also due to the depletion of B level population. The photoconverted B molecule produced corresponding enhancement of the population in the M-state leading to the observed enhancement of absorption at 410 nm. The population from the M-state relaxes into the O-state leading to the enhancement of the absorption at 640 nm. The pump beam intensity-induced variations in the absorption characteristics of bR film at various probe wavelengths predicted by the present analysis match very well with recent experimental results¹⁸.

In conclusion, we have applied the simplified model proposed earlier for the complex photocycle of the bR molecule to model the photocycle of D85N, a genetic variant of bR which exhibits an additional long lifetime intermediate P(Q)-state ideal for making volumetric memories. Analytical expressions for the transmission characteristics of bR films at different probe wavelengths are derived using the rate equation approach. These results are very useful for designing the molecular SLMs based on the intermediate states of the D85N variant of bR molecules.

---

1. Birge, R. R., Annu. Rev. Phys. Chem., 1990, 41, 683–733.
2. Osterhelt, D., Brauchle, C. and Hampp, N., Q. Rev. Biophys., 1991, 24, 425–478.
3. Birge, R. R., Am. Sci., 1994, 82, 348–355.
4. Huang, J. Y., Chen, Z. and Lewis, A., J. Phys. Chem., 1989, 93, 3314–3320.
5. Peda’el, A., Daisy, R., Horowitz, M. and Fischer, B., Opt. Lett., 1998, 23, 1173–1175.
6. Werner, O., Fisher, B., Lewis, A. and Nebenzahl, I., Opt. Lett., 1990, 15, 1117–1119.
7. Rao, D. V. G. L. N., Aranda, F. J., Wiley, B. I., Akkara, J. A., Kaplan, D. L. and Roach, J. F., Appl. Phys. Lett., 1993, 63, 1489–1491.
8. Reddy, K. P. J., Appl. Phys. Lett., 1994, 64, 2776–2778.
9. Rayfield, G., Phys. Bull., 1989, 34, 483.
10. Haronian, D. and Lewis, A., Appl. Opt., 1991, 30, 597–608.
11. Song, Q. W., Zhang, C., Blumer, R., Gross, R. B., Chen, Z. and Birge, R. R., Opt. Lett., 1993, 18, 1373–1375.
12. Reddy, K. P. J., J. Appl. Phys., 1995, 77, 6108–6113.
13. Joseph, J., Aranda, F. J., Rao, D. V. G. L. N., DeCristofano
    B. S., Kimball, B. R. and Nakashima, M., Appl. Phys. Lett., 1998, 73, 1484–1486.
14. Joseph, J., Aranda, F. J., Rao, D. V. G. L. N., Akkara, J. A. and Nakashima, M., Opt. Lett., 1996, 21, 1499–1501.
15. Rao, D. V. G. L. N., Aranda, F. J., Rao, N. D., Chen, Z.,
    Akkara, J. A., Kaplan, D. L. and Nakashima, M., Opt. Commun., 1996, 127, 193–199.
16. Korchemskaya, E. Y., Soskin, M. S. and Taraneko, V. B., Sov. J. Quantum Electron., 1987, 17, 450–454.
17. Ludmann, K., Gergely C., and Varo, G., Biophys. J., 1998, 75, 3110–3119.
18. Popp, A., Wolperdinger, M., Hampp, N., Brauchle, C. and Osterhelt, D., Biophys. J., 1993, 65, 1449–1459.
19. Birge, R. R., Sci. Am., 1995, 272, 66–71.
20. Downie, J. D., Timucin, D. A., Smithey, D. T. and Crew, M., Opt. Lett., 1998, 23, 730–732.
21. Hampp, N. and Zeisel, D., IEEE Eng. Med. Biol., Feb./March, 1994, 67–74.
22. Chen, Z., Lewis, A., Takei, H. and Nebenzahl, I., Appl. Opt., 1991, 30, 5188–5196.
23. Varo, G., Duschl, A. and Lanyi, J. K., Biochemistry, 1990, 29, 3798–3804.
24. Lindvold, L. R. and Ramanujam, P. S., J. Sci. Ind. Res., 1995, 54, 55–66.

 ACKNOWLEDGEMENT.  S.R. is grateful to DST for the award of the SERC Visiting Research Fellowship during this work.

Received 31 August 1999; revised accepted 29 October 1999